算法图解

算法简介

算法只是一组完成任务的指令，任何代码片段都可以视为算法；

二分查找

当数据是有序的时候，使用二分查找可以在对数时间内得到结果；

对数是幂运算的逆运算

大 O 表示法

大 O 表示法用来表示算法运行时间的增速；

注意：它是代表增速；

  • O(log n)：对数时间
  • O(n)：线性时间
  • O(n * log n)
  • O(n^2)
  • O(n!)

选择排序

当要在内存中存储多项数据时，需要用到数组或者链表的数据结构；

数组

  • 使用数组时，意味着数据在内存必须是连续存放的；因此，当给数组添加元素，导致超过可用连续段的数据时，则需要重新寻找一个新的连续段，并将数据复制过去；
  • 一个折中的办法是提前预留一些空间，这样可以避免降低转移的机率，代价是浪费一些空间；即以空间换时间；
  • 数组的优点是访问速度快，但插入速度有可能比较慢（当发生转移的时候，或者例如把元素插入在头部的时候）；

由于使用虚拟内存映射物理内存，当虚拟内存发生转移的时候，或者有可能物理内存的内容不需要发生转移，只需要更改页表的映射即可？

链表

  • 使用的链表的好处则在于当添加新元素时，完全不需要移动旧元素的位置；只需随便找个空位置存放新数据，然后将地址放在上一个元素中即可；
  • 链表的优点是插入速度快，但访问速度慢；但如果刚好是要读取所有元素，则链表的效率还是很高的；

数据结构

所谓的数据结构，其实跟内存有很大的关系，当数据存放在内存中的时候，需要有一种地址计算机制，以便找到这些元素；

  • 数组通过记住头元素的地址，然后按顺序索引的方式计算出另一个元素的地址；
  • 链表通过头元素的地址，顺序向下查找，直到找到所需的元素；

    对于二叉树，其实现机制是否让每个元素存放左右两个分支的地址，分别代表某种条件判断真假后的相应分支？待验证；

数组和链表各有其优缺点，因此还可以通过将二者进行结合的方式来存储数据，这样可以兼顾二者的优点；

选择排序

每次遍历一轮，从中挑出最大或者最小的元素，放入一个有序的新列表中；

这种方法的缺点是需要遍历很多轮，导致运行时间为 O(n2)；有没有可能只遍历一轮，然后通过建造一个二叉树的方式，来存放遍历结果？在纸上试画了一下，貌似不太行；

递归

  1. 栈也是一种数据结构，以前没有太明白这句话的意思，但当它和数据存储以及寻址提取的需要进行联系时，它就变得非常容易理解了；对于栈的使用，我们只需要记住栈顶的指针，压栈和出栈的时候，向不同的方向改变栈顶指针的地址即可；
  2. 函数在返回的时候，需要将原调用者中断指令的地址，发给程序计数器，以便接下来跳转到中断处继续执行原调用者余下的指令，同时，还要改变栈顶的指针，使其指向原调用者的栈桢的顶部；而在一开始时调用函数的时候，除了发生了跳转外，还需要有保存当前指令的地址到栈中，而被调用的函数，会将栈指针（即栈桢的顶部地址）保存到寄存器 %ebp 中；
  3. 出栈和入栈的动作，在指令的眼里，实际上是通过 add 和 sub 来改变栈顶指针数值大小的动作；通过 add 和 sub 来申请和释放栈空间；
  4. 栈是一块动态分配的内存空间，用来存储一些临时的数据；栈被划分成多个栈桢，每个栈桢对应一次函数调用，栈桢中存储着该次函数调用的一些临时变量；每个栈桢有一个顶部地址（栈指针）和底部地址（桢指针）；当分配新栈桢的时候，原栈桢的顶部地址，就变成了新栈桢的底部地址；CPU 中有两个寄存器 %esp 和 %ebp，分别存储着当前栈的顶部和底部的指针值；
  5. 当发生函数调用的时候，会将函数参数、返回地址、桢指针值，放在当前栈桢的顶部，然后进入下一个新栈桢；事实上，所谓的栈桢也只是逻辑上存在的，编译器小心的维护桢顶和桢底的地址来实现相应的目的；
  6. 寄存器的空间是有限的，为了在这有限的空间内，完成每一次的函数运算，它需要内存（虚拟内存）配合，帮忙保存一些状态数据和中间数据，这样 CPU 才可以完成不同函数之间的调用和返回的切换；而栈的使用以及栈顶和栈底指针，可以让代码使用相对地址进行偏移量计算，因为有些变量的长度是动态的，所以并不能在编译的时候直接使用绝对地址；

快速排序

  • 分而治之的策略（想起了费曼技巧，将大问题拆解成小问题）；
  • 欧几里得算法：求两个整数 A 和 B 的最大公约数 GCD(A, B)，可以转换为求 A/B 的余数 与 B 的最大公约数，假设 A = B * n + R，则 GCD(A, B) = GCD(B, R)；

递归算法

  • 定义基线条件；
  • 缩小问题规模，直到其符合基线条件；

编写涉及数组的递归函数时，基线条件一般是空数组或只包含一个元素；

快速排序

选择一个基准值，将数组拆分成比它小和比它大的两组，然后对每一组各自进行递归，并合并最后的结果；

  • 快速排序平均运算时间为 O(n * logn)，最糟糕的情况是 O(n * n)，最佳情况是 O(logn)；
  • 合并排序的运算时间固定为 O(n * logn)；表面上看貌似比快速排序更好，但事实上其单次的运算时间比快速排序多，导致最后的总运算时间比快排多；
  • 大 O 表示法中所谓的运算时间，其真实含义其实是运算次数；但不同算法的单次运算所需的时间有可能是不同的；

散列表

  1. 散列函数：无论给这个函数什么样的输入，它都会输出一个数字；
  2. 散列表的其他名称：散列映射、映射、字典、关联数组；
  3. 问题：对于 Python 中的字典来说，它如何确保不同的键名的散列数字不会冲突？答：冲突不可避免，解决方法有多种；其中一种方法是在存储位置放置一个链表，来拓展可存储的空间；但链表也不适宜太长，不然会降低搜索性能，当链表很长的时候，需要采用其他方法，甚至重新设计散列表本身的长度，同时确保它的散列结果均匀分布；
  4. 问题：猜测散列表是一种用空间换时间的方法？

散列函数的实现

  • 散列表使用数组来存储数据；既然是数组，意味着其存储空间是连续的；当需要存储的数据个数，超过了预分配的空间时，可能会发生迁移的情况？答：没错，它使用装填因子来触发迁移，一般控制在 0.7；当超过0.7时，就将数组的长度增加为原来的2倍；
  • 填装因子：要存储的数据个数 / 数组的长度；填装因子越小，发生冲突的概率就越低；

广度优先搜索

  1. 解决最短路径问题的算法，一般使用广度优先搜索；使用图来建立数据模型，使用队列建立搜索列表；
  2. 图由节点和边组成，它用来描述哪些节点与哪些节点之间存在连接；
  3. 当有了节点和边后，可以通过搜索一个节点所关联的第1级节点，第2级节点……第n节点，来判断一些想要的结果；例如先搜索自己的朋友，再将朋友的朋友也加入搜索的范围；这便是广度优先搜索；（听上去像是一种暴力算法）
  4. 有向图：节点间的关系是单向的，图中的边会带有箭头；无向图的边则没有箭头；
  5. 广度优先搜索的运算次数为 O(v+e)，其中 v 表示 vertice 节点数，e 表示 edge 边数；
  6. 树也是一种图，只是这种图比较特殊，它没有往回指的边；

狄克斯特拉算法

广度优先算法可以用来寻找边数最小的路径；狄克斯特拉算法可用来寻找消耗时间最短的路径（相当于给边分配了权重，然后找出总权重值最小的路径）

狄克算法描述

从起点出发，罗列出所有余下节点的权重开销，对于不可达的节点，设定其开销为无穷大；依次遍历开始位置的节点的邻居，计算其到达余下节点的开销（需计入起点到当前节点的历史开销），如有比原开销更短的路径，更新其开销；重复该步骤，直到遍历完所有节点；

  • 有权重的图称为加权图，没有权重的图称为非加权图；
  • 无向图中，每条边都是一个环，狄克算法只适用于有向无环图；
  • 狄克算法有一个基本假设，即已经处理过的节点，没有前往该节点的更短路径，这种假设仅在没有负权重边时才成立；因此狄克算法不能用于处理有负权边的情形；此时需要使用贝尔曼-福德算法；

狄克算法实现

数据结构

  • 新建一个子节点散列表，保存每个节点及其邻居（作为节点的属性，并将权重做为属性值）；
  • 新建一个开销散列表，保存到达当前节点的最短路径开销；
  • 新建一个父节点散列表，保存每个节点的最短路径父节点；
  • 新建一个节点数组，记录已经处理过的节点；

算法实现

  1. 遍历所有未处理的节点；
  2. 计算每一个未处理节点，到达下一个邻居节点的累积路径开销；
    1. 如果当前节点到达下一个邻居节点的路径开销，比现已知的到达该邻居节点的路径开销更小，则更新开销表中下一个节点的最短路径开销值；
    2. 遍历完当前节点的所有可达邻居节点后，将当前节点加入已处理列表中；
  3. 重复第二步，计算下一个未处理节点；

贪婪算法

  1. 贪婪算法：每步采用局部最优解，以期最终得到全局最优解；虽然最终不一定能得到，但会相当接近；因此，贪婪算法不是完美答案的算法，但是一种简单的算法；
  2. 旅行商问题：找出最短路径的组合；
    1. 随便选择一个出发城市
    2. 选择出发去下一个城市时，选择最近的还没有去的城市；
  3. 集合覆盖问题：找出覆盖所有州的最小电台集合；
    1. 从剩余可选电台中，找出覆盖最多未到达州的电台，放入候选列表；
    2. 重复第一步；
  4. 判断是否 NP 完全问题的一些潜在迹象
    1. 涉及所有组合；
    2. 随着元素数量增加，计算量急剧上升；
    3. 不能将问题分解成小问题；
    4. 涉及序列且难以解决（如旅行商问题）；
    5. 涉及集合且难以解决（如电台问题）；
    6. 可转换为集合覆盖问题或旅行商问题；
  5. 对于 NP 完全问题，最佳的做法是使用近似算法；
  6. 找出满足球队最佳组合的球员，原理也跟电台问题一样；

动态规划

  1. 动态规划原理：先解决小问题，再解决大问题；可用来寻找给定约束条件下的最优解；每种动态规划方案都涉及网格，每个单元格都是一个子问题；根据问题不同，计算动态规划方案的公式不同，没有统一的公式，需要根据问题定制化设计；
  2. 案例：4公斤的背包，偷盗最有价值商品的组合；
    a64732e8403d03346a339f06a97a0358.png
  3. 方法：先找出背包容量只有1公斤、2公斤、3公斤等情况下的最佳组合（即大问题先转换为小问题来解决）；然后在4公斤的时候，就可将其转换成当前新选择+余下容量最佳组合的和，来得到最终解；如果新选择的容量和没有大于旧选择的容量和，则以旧选择为准，放弃新选择；
  4. 如果商品单位不是整件，而是可以部分，例如大米，则动态规划算法不适用，但此时可以使用贪婪算法；
  5. 动态规划算法的前提是各个选项之间是独立的，不存在相互依赖的关系；如果某些选择之间有依赖关系，则动态规划方法不适用；
  6. 单词最匹配预测：寻找最大公共子串问题；
    1. 既然是公共子串，那意味着最低限度也要有一个字符相同，这样才谈得上有公共的部分；
    2. 当有一个字符相同时，如果前面还有一个相同的字符，则构成了2个相同字符的字串；如果前面的字符不同，则只构成一个相同字符的子串；
    3. 最长公共子串不一定出现在单词的末尾，它也可以出现在单词的中间；
  7. 单词最匹配预测：寻找最大公共子序列问题：与寻找最长公共字串的算法略有不同：
    1. 当存在一个相同字符时，该单元格标注为左边或上边邻居中较大的值加1；
    2. 当存在不同的字符时，该单元格标注为左边或上边邻居中较大的值；

K最近邻算法

  1. K最近邻算法即 KNN，全称 K nearest neighbor；
  2. 当要给某个东西分类时，查看离它最近的3个邻居，如果其他有2个邻居是 A 类物品，则该东西很可能是 A 类物品；
  3. 如何计算 A 和 B 点的距离？将物品进行特征建模，每个特征做为一个维度，这样物品就可以转换成空间维度中的坐标，然后使用勾股定理计算两点之间的距离；
  4. KNN 可以用来实现两项基本工作：分类（即分组）和回归（即预测结果）；
  5. 计算相似度除了使用距离来比较，还可以使用余弦相似度来比较，它比较的是角度，而不是距离；当每个人打分的标准不同时，使用余弦相似度会更加适合；
    1. 余弦相似度与向量的长度无关，而只是方向有关，它的取值在 -1 到 1 之间；当夹角为0度是，相似度为1；当夹角为90度时，相似度为0，当夹角为180度时，相似度为 -1；
  6. 对于 KNN 算法，挑选合适的分类特征很重要，需要确保这些特征能够准确反应事物的属性，同时又与要解决的问题相关；
  7. OCR、语音识别、人脸识别都是使用 KNN 算法原理；它从数据集中提取特征，然后根据特征建模，找到分类标准；这样当有新的数据进来时，提取新数据的特征，依据标准对数据进行分类；
  8. 依据特征统计分类标准的过程，即为训练；
  9. 朴素贝叶斯分类器 Naive Bayes Classifier；
    1. 朴素贝叶斯常用于文本分类领域；文本分类一般以词频为特征，判断文件所属的类型（例如垃圾邮件、政治、体育、合法等）；

接下来如何做

树

有序数组的优点是查找非常快，平均都是 O(logN)，但它的缺点是插入和删除非常慢，平均都是 O(n)；为了克服这种缺点，引入了二叉查找树的数组结构，它的特点是每个节点都两个子节点，左边节点存储比它小的值，右边节点存储比它大的值；对于二叉树，它的平均查找、插入、删除的时间都是 O(logN)（当然，前提是这是一棵平衡的二叉树，如果不平衡，而性能达不到 O(logN)；

  • 数据库和文件系统常使用 B 树来存储数据；它适用于读写相对大的数据块，因为 B 树的节点支持一定的范围的关键字，刚好跟磁盘读写单元块相对应，所以读写效率比其他树结构来得高；
  • 其他常用的树结构还包括：红黑树、伸展树、B+树、B* 树等；

平衡二叉树（AVL树）

  • 每个节点最多允许拥有2个子节点；
  • 左子节点的值小于当前节点，右了节点的值大于当前节点；
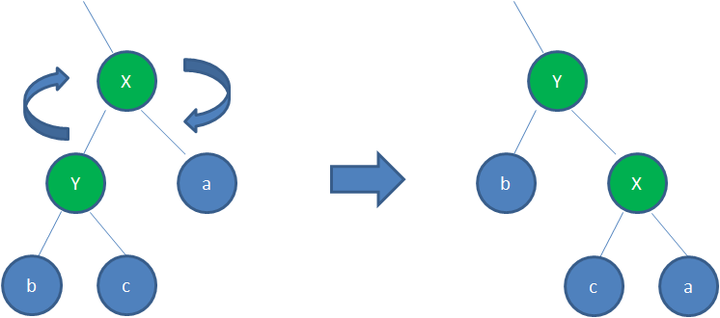
  • 左右两边的节点层级差不大于1（如何做到？通过对树进行左旋或者右旋来实现）
左旋

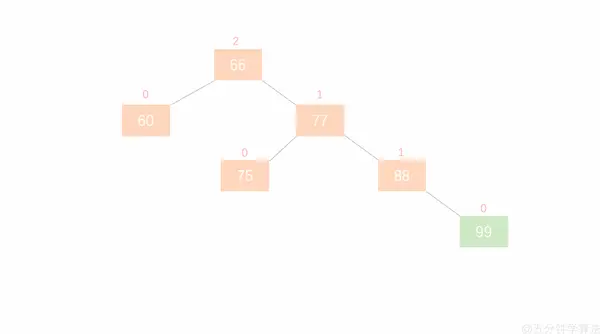
image

右旋

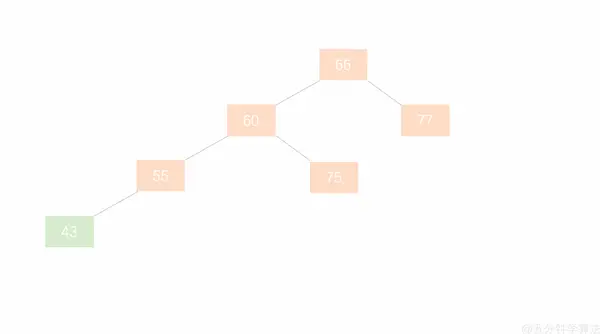
image

B 树

一种自平衡的树（不二叉，而是多叉），能够保持数据有序；

  • B 树的每个节点可以拥有2个以上的子节点；
  • 子节点的数量范围预先定义好（例如 2-4 B树，表示允许 2-4个子节点）
  • 当发生数据插入或删除时，如果超过范围，会触发内部节点的拆分或合并；拆分或合并后都需要满足左边节点本身比左边节点大，比右边节点小的排序规则；
  • 由于有一定的范围，所以不需频繁的调整以保持平衡；
  • 但缺点是节点可能没有完全填充，会浪费一定的空间（以空间换时间）；
  • 节点除了存储关键字外，还需要存储子节点的地址；二者的数量差不多均分；
查找示例

查找字母 E，则依次比较根节点M，然后二级节点DG，盱 D<E<G，所以沿中路分支，在三级节点查到 E；
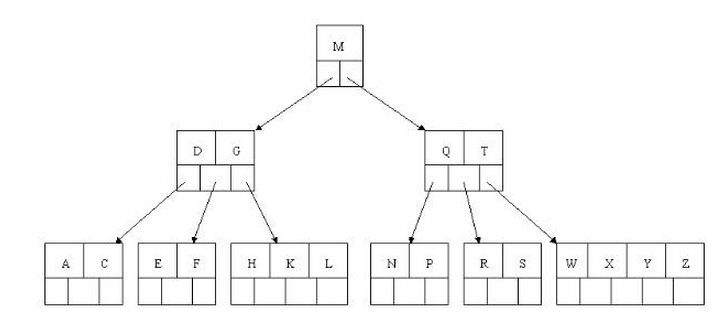
image

插入示例

假设要构建的为 5 阶树，则当关键字必须<=(5-1)即小于等于4，意思是当关键字数超过4时，需要进行节点拆分；现在模拟插入3、8、31、11、23、29、50、28

先插入 3、8、31、11

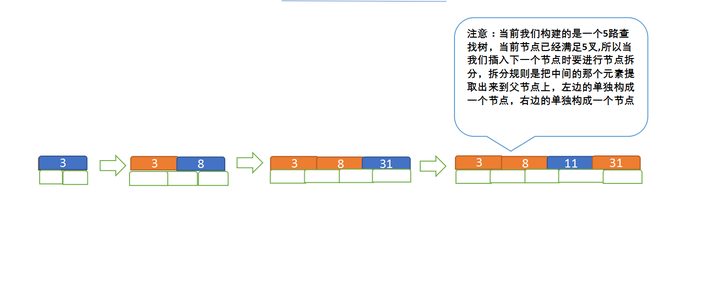
image

再插入23、29

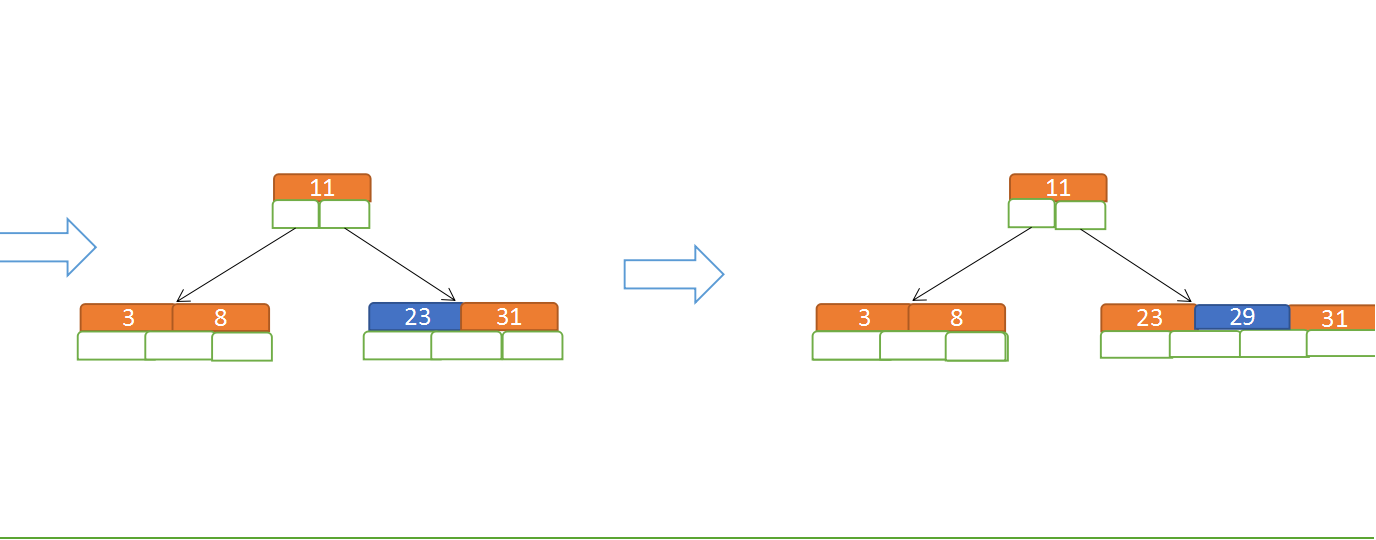
image

再插入50、28

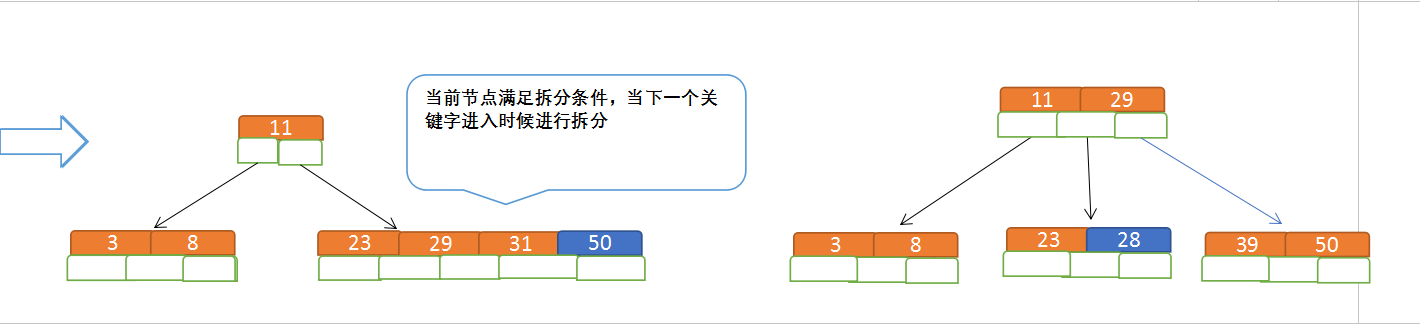
image

删除示例

假设为5路查找树，由于 m = 5，因此关键字数必须 >= (ceil(5/2) -1) 为 2，所以当关键字小于2时，会触发合并；

删除数字 28

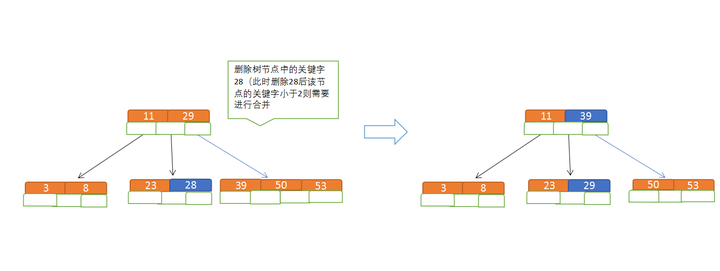
image

B+树

B 树的升级版，由于更充分的利用了节点的空间，使得其查询速度更快；

与 B 树的区别如下：
  • 非叶子节点不再保存关键字，只保存索引值和子节点地址；这样每个节点可保存的数据就增加了很多；
  • 查找时，根据索引值判断应选择的子节点分支；
  • 由于每个子节点可保存的内容变多，导致树的高度层级变少，所以查询性能更好；
  • 所有数据都存储在叶子节点上；而且由于是有序的，所以遍历全表的时候，只需扫描所有叶子节点即可，不用遍历非叶子节点；方便数据库做全表扫描；
  • 同时在查询大小区间的数据时，也更方便；

B* 树

B* 树是 B+ 树的变种，它与 B+ 树的区别有两点：

  • 当某个节点满了后，它不会马上拆分，而是会先检查一下兄弟节点是否已满；
    • 若未满，则向兄弟节点转移元素；
    • 若已满，则进行拆分；从自身和兄弟节点中，各拿出三分一的元素来组成一个新的节点；
  • B* 树每个节点存有兄弟节点的指针；

由于有向兄弟节点转移元素的功能，使得 B* 树的拆分频率比 B+ 树要小一些；

红黑树

红黑树是另外一种自平衡的二叉树；

  • AVL 树的约束是高度差不大于1，这样会导致插入或删除时频繁发生旋转；红黑树则放松了这方面的限制，它通过引入颜色属性，并增加一些与颜色相关的约束条件来控制平衡；
  • 红黑树通过牺牲了部分平衡性，来换取插入/删除操作时更少的旋转操作，从而在整体上性能优于 AVL 树；
  • 约束条件：
    1. 根节点必须是黑色的；
    2. 所有 NIL 叶子节点也都是黑色的；
    3. 每个红色节点必须有两个黑色的子节点；
    4. 从叶子节点到根节点的路径上，不能有两个连续的红色节点；
    5. 任一节点到其每个叶子的所有路径都包含相同数目的黑色节点；
    6. 虽然红黑树的插入/删除触发的旋转不如AVL频繁，但是一旦触发，其引起的颜色变更和旋转要复杂得多，但操作时间仍可控制在 O(log n) 次；
  • 字典据说主要使用红黑树来实现，好奇是如何做的？
变色

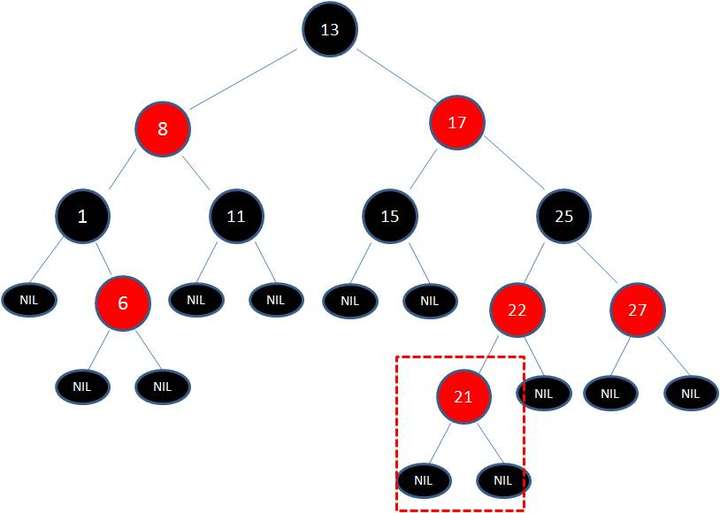
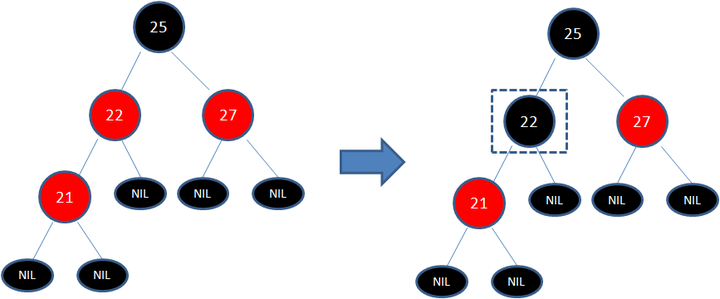
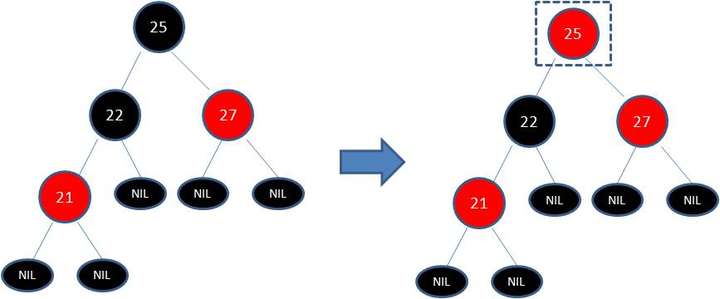
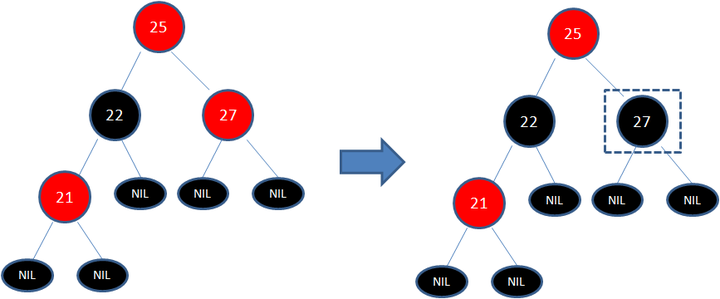
image
image
image
image
image

左旋

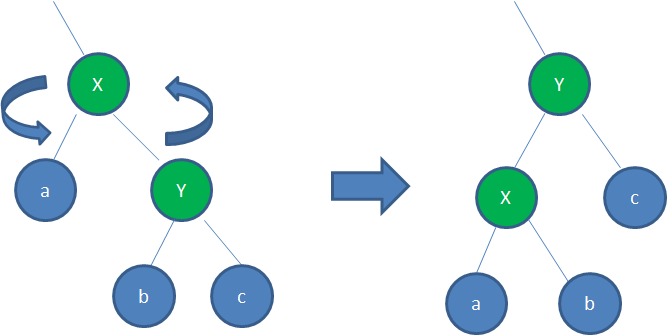
image

右旋

image

伸展树

  • 伸展树也是一种自平衡的二叉树；它基于理念：越是被频繁访问的元素，应该离根节点越近，以便提高查找速度；
  • 因此，每次查找后，伸展树会进行一系列旋转操作，让被访问节点更靠近根节点；
  • 优点：性能不输于平衡树；存储空间小（因为不需要存储保持平衡的额外信息）；
  • 缺点：在极端情况下会变成链；在多线程的情况下会变得很复杂；

反向索引

  • 正向索引是通过键找到值，反向索引是对值进行排序，然后根据值找到键；
  • 它可用来做为网页搜索引擎的算法；对搜索的关键字进行反向索引，当用户输入关键字后，根据关键字索引，查找到包含这些关键字的网页；

傅里叶变换

  • 作用类比：
    • 给它一杯冰沙，它可以告诉我们其中包含哪些成分；
    • 给它一首歌曲，它可以告诉我们其中包含哪些频率；
  • 傅里叶变换很适合用来对各种信号进行处理，包含音乐、图片、各种波等；

并行算法

并行算法的设计

并行算法的设计需要考虑两个问题

  • 并行性管理：如何合并并行计算的结果；
  • 负载均衡：确保任务分配相对均匀，各自的任务完成时间大致相同；
MapReduce

一种分布式算法，可以将计算任务分配到多台计算机上分布计算；

  • Map 函数（映射）：接受一个数组，对里面的每个元素进行相同的处理；
  • Reduce 函数（累计）：将每次的处理结果进行累计；

布隆过滤器

可用于判断某个元素是否存在于某个巨大的集合中；

  • 优点：需要的存储空间比散列表小很多；
  • 缺点：它可能会出现错报（伪阳性，false positive），但不会漏报（伪阴性，false negative）；
  • 原理：初始化一个长度为 m 的位数组，挑选 k 个哈希函数，用来将输入值转换成 k 个位结果；
  • 查询过程：判断哈希函数生成的每个位结果，在 m 数组中相应的位上的值是否为 1，若都为 1，则表示值可能存在于集合中；若有一个为 0，则表示值在集合中一定不存在；
  • 写入过程：根据哈希函数生成的每个位结果，将 m 数组中相应的位上的值置为 1；

哈希函数的数量 k，以及数组的长度 m 会涉及误报率 p；m 越大，k 越小，则 p 越小；m 越小，k 越大，则 p 越大；

k/m/p 的关系

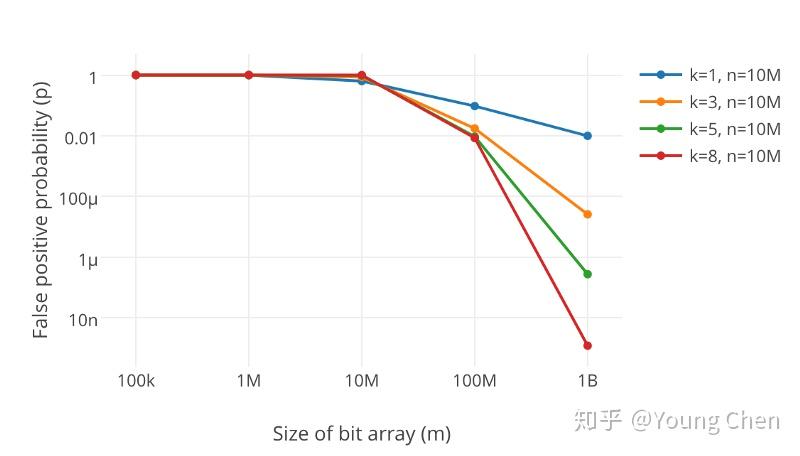
image

k/m 计算公式

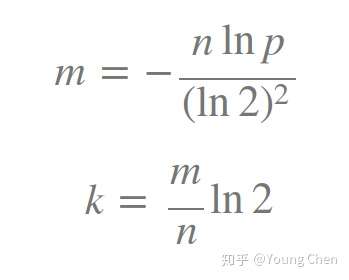
image

感觉布隆过滤器很像 bitmap，差别在于 bitmap 适用于连续型的数据，因此不需要哈希函数；而布隆则适用于任意类型的数据；

HyperLogLog

HyperLogLog 主要用于基数计数的场景；

  • 基数计数(Distinct Value)：统计一个集合中不重复的元素个数；例如网站的日活跃 UV 统计、某日搜索的关键词个数统计等；常用方法是设计一个散列表，每次新来的一个元素，判断是否在集合中；若不在则新增，若存在则增加计数；这种方法准确率100%，但需要完整的内存存储空间来存放集合中的每一个元素；
  • 优点：相比散列表， HLL 非常节省内存；
  • 缺点：它是一种概率算法，有一定的概率会误报；但结果基本准确；

例如对于 10^9 的基数，只需 1.5KB 的内存，即可实现 2% 标准差的统计结果；

问题模拟

数据库中有某日访问某个页面的访问记录，记录的字段包含有用户名，部分用户存在多次访问该页面的情况，求：共有多少个不重复的用户在该日访问了该页面？

问题解法

暴力法

计算出每条记录中的用户名的哈希值；
从所有的哈希值寻找最大的连续0的个数，假设为 k；
根据 k 算得该页面不重复的访问用户数量约为 2^(k+1)

这个解法并不准确，不能应对极端事件，例如当1000万次访问全部是由一个用户请求的时候；

分桶法
  • 将每个哈希值分成两段，第一段做为桶的编号，第二段用来计算k（即连续0的个数）
  • 假设分成了10000个桶，最后 k 取这10000个的平均值；
  • 假设1000万次访问全部是一名用户，则所有的记录都会被分成到一个桶，剩下的9999个桶的 k 值都为 0，因此计算出来的 k 的平均值就会变小很多；桶数越大，k 值的偏差越小；
  • 基数估计 = 桶数 * (2 ^ 平均 k)

79980d865579094731a4aa5200c9f340.png

m 代表桶数；
R 代表均值 k；
constant 代表常数，用来修正（其计算公式附后）；

分桶法改进

在分桶法中，k 使用平均值，但平均值的缺点是容易受到一些极端数值的影响；为了避免这个缺点，改为使用调和平均法，来求取 k 值；

46d4b65feaf8c4c6f0d037c544aff223.png

Hn 代表 2^(调和平均 k 值)；
xi 代表单次的基数估计值，它等于 2^(ki + 1)；
n 代表总的桶数 ；

改进后的基数统计公式如下：
433ced54c262f01a2dfe0744f8fbbfd0.png

当数据量很小的时候，上面的公式计算出来的结果偏差会比较大，因此需要引入一个条件判断，当数据量小于某个临界时，使用其他计算方式

1
2
3
4
5
if DV < (5 / 2) * m:
    DV = m * log(m/V)
# V 代表结果为 0 的桶的数量；
# m 代表桶数；
# DV 代表按前面的公式计算出来的结果
桶数 m 的选择：

根据想要控制达到的相对标准差值 RSD（relative standard deviation）来计算：
d65e70fae37f5ff608766b213f377540.png

常数 constant 的选择：

c961e1e758069bb58757fd91bd664d1a.png

m 表示桶数

1
2
3
4
5
6
7
8
9
10
switch (p) {
   case 4:
       constant = 0.673 * m * m;
   case 5:
       constant = 0.697 * m * m;
   case 6:
   
       constant = 0.709 * m * m;
   default:
       constant = (0.7213 / (1 + 1.079 / m)) * m * m;}

SHA 算法

在创建散列表时，里面会用到某种散列函数，它会将一个键名，转成一个索引，从而能够在 O(1) 的时间内，找到值存储的位置；

用途

  • 比较文件：使用同一个散列函数，计算两个文件的散列值；如果值相同，则意味着这两个文件相同；
  • 检查密码：服务器不存储用户的密码，而是存储其密码的散列值，这样即使服务器上面的密码被泄露，也不会导致用户的密码暴露；

SHA 算法包括 SHA-0, SHA-1, SHA-2, SHA-3，前两个被证明有缺陷，一般使用后两个；

局部敏感的散列算法

散列函数默认是局部不敏感的，即输入值即使只有细微的差异，输出值都会有巨大的不同；但有时候也需要局部敏感的散列函数，用来判断两个事物是否非常相似；

用途

  • Google 判断某个网页是否已经收集；
  • 判断论文是否抄袭；
  • 判断用户上传的文档或图书是否侵犯了版权；

Diffie-Hellman 密钥交换

即公钥和私钥，发信人使用公钥进行加密；加密后的内容只有私钥持有者才能打开；

Diffie-Hellman 算法的替代者为 RSA 算法；

线性规划

用途：在给定约束条件下最大限度的改善指定的指标；

例子

  • 有限的原材料，生产两种产品，如何获得利润最大化；
  • 有限的时间和资金，在两个不同的州分别获取选票，如果将选票数量最大化；

所有的图算法都可以使用线性规划来实现，图问题只是其中一个子集；
线性规划使用 Simplex 算法；

计算机
#算法
算法图解
https://ccw1078.github.io/2019/10/24/算法图解/
作者
ccw
发布于
2019年10月24日
许可协议